A new random number generator for Parallel and Distributed systems¶

Pseudo Random Number Generators, or PRNGs, are used in many different types of applications. Scientific applications that simulate a particular phenomena make use of PRNGs extensively. These types of applications often require PDC techniques to get the performance they need to run large simulations.

In this chapter we are going to justify the need for using correct random number generators that work in parallel code using either shared memory threads with openMP or processes with MPI. Then we will demonstrate one particular library that correctly generates a proper distribution of random numbers for code using either of these software libraries.

Properties of Pseudo Random Number Generators¶

How to use mathematics to generate a stream of random numbers has been studied extensively for quite some time, longer for the sequential single thread/processor case (since 1969) than for various PDC hardware and software libraries (as early as 1986). The mathematics involved in properly generating a stream of numbers from a given starting point called a seed are beyond the scope of this chapter. We will instead focus on the properties that these well-studied methods should possess.

For computational purposes, PRNGs create one random value at a time when requested. The entire set of numbers generated (in a for loop, for example) is often referred to as the stream of numbers.

A good sequential or parallel PRNG method must have these properties:

Uniformity: The numbers generated through the range of values requested are uniform.
Independence: Any value drawn next is independent of the previous value.
Efficiency: The generation of the next number should be fast.
Long Cycle length: For a large stream in a wide range, it should take a long time before numbers repeat.
Reproducibility: From a given starting seed, the same set, or stream of numbers should be generated. This property is helpful for debugging, but constant seed values should not be used in applications.

Really good parallel PRNGs require all of these properties, along with the following:

Fair Play: Regardless of the number of threads/processes (processing units, or PUs), the same set of values is generated as in the stream generated by a sequential algorithm with the same starting seed.

In this chapter we will use a freely available C++ PRNG library called trng (for Tina’s random number generator). The site for this library contains extensive documentation and additional code examples if you would like to delve deeper. The trng library, as you will discover, possesses the above properties.

Note

The code in this section is C++ code. Even if you have mainly coded in C, these examples are fairly straightforward and accessible, since they are written in C style for the most part.

Sequential Random Number Generation with trng¶

Let’s first examine how we can use the trng C++ library to create a sequential version of code (running on one process) that uses a loop to generate one value after another in a stream.

This is the main program that sets up the use of the random number generator and uses a uniform distribution of integers from 1 to 99 for the values in the stream. Study it carefully to see how we use trng to do this.

#include <stdio.h>        // printf()
 #include <time.h>        // time()

// separate code for handling command line arguments is below

#include <trng/yarn2.hpp>  // trng YARN (yet another random number) generator class
 #include <trng/uniform_dist.hpp>   // we'll use a uniform distribution
                                 // of the random numbers

////////////////////////////////////////////////////////////
 int main(int argc, char* argv[]) {

// set up what conditions we will use:
     //  - defult size of repetitions in the loop
     //  - whether to use a constant seed so we can repeat and
     //    get same random values in stream
     //  - fixed range of random numbers from 1 to 99
     int repetitions = 8;
     int useConstantSeed = 0; // for same stream, set this to 1 on cammand line with -c

// range for uniform distribution of random numbers
     int min = 1;
     int max = 99;

// gather command line arguments
     getArguments(argc, argv, &repetitions, &useConstantSeed);

// ////////////  random generator setup //////////////////////////

// random numbers start from a seed value
     long unsigned int seedValue;  // note for trng this is long unsigned

// same constant seed will generate the same sequence of rndom numbers
     // use for testing to varify same sequence regardless of number of threads
     if (useConstantSeed) {
         seedValue = 888777666;
     } else {  // variable seed based on computer clock time
         seedValue = (long unsigned int)time(NULL); // enables variation; use for simulations
     }
     // number generation needs two things: a generator and a distribution of the numbers
     // declare the generator object
     trng::yarn2 randGen;
     // declare the distribution to use (here it is uniform with vallues in the range min to max)
     trng::uniform_dist<> uniform(min, max);

// Set the starting point of the generator by seeding it
     randGen.seed(seedValue);

// //////////////// end PRNG setup ////////////////////////////////////

// /////////////// get a portion of the stream /////////////////////////
     int nextRandValue;   // holds the next value as we go through the loop

// loop to get each number in the PRNG stream and print it
     // Note here the ubiquitous for loop construction of incrementing by 1
     int i;
     for (i=0; i < repetitions; i++) {
         // get next number in the stream from the distribution
         nextRandValue = uniform(randGen);
         // print tid(i):nextRandValue
         printf("t0 (%2d):%2d \n", i, nextRandValue);
     }

}

There are several points to notice about this code:

We declare both a generator object (randGen, line 44) and a type of distribution of the numbers (uniform, line 46). There are other types of distributions of numbers that are useful in many applications, but we will not cover those here.
The syntax of the declaration of the distribution requires that we give it a minimum and maximum value for the range of numbers. The range includes the minimum, but not the maximum.
A seed value is declared as a long unsigned int.
Before requesting numbers from the stream, we first seed the generator (line 49).
To get the next number inside the loop, we call the constructor for the object called uniform and send it the generator object (line 61). Since we declared nextRandValue an int, the use of uniform(randgen) will return an int. This is a nice feature of this C++ library.

If you run it without any changes, it is running with these command line arguments:

-c means use a constant seed. From this if you repeat a run you should get the same stream of numbers. This shows that this generator is reproducible, which you will see is very handy when debugging your code.
-n 8 indicates to generate 8 numbers (repeat the loop 8 times).

You should try it without the -c and run it a few more times to see that a new set of values is generated each time when we seed with a different number each time.

If you are interested in the code for handling these arguments for this sequential version, you could study the following code block. It is included with the code above when it is run, and not intended to be run on its own.

#include <stdio.h>
 #include <unistd.h>
 #include <stdlib.h>
 #include <ctype.h>

void getArguments(int argc, char *argv[],
               int * N, int * useConstantSeed);

int isNumber(char s[]);
 void exitWithError(char cmdFlag, char ** argv);
 void Usage(char *program);

void getArguments(int argc, char *argv[],
                 int * N, int * useConstantSeed)
 {
     int c;        // result from getopt calls

// The : after a character means a value is expected
     // No colon means it is simply a flag with no associated value
     while ((c = getopt (argc, argv, "n:hc")) != -1) {

// getopt implicitly sets a value to a char * (string) called optarg
     // to what the user typed after -n
         switch (c)
         {
         // character string entered after the -N needs to be a number
         case 'n':
             if (isNumber(optarg)) {
             *N = atoi(optarg);
             } else {
             exitWithError(c, argv);
             }
             break;

// If the -h is encountered, then we provide usage
         case 'h':
             Usage(argv[0]);
             exit(0);
             break;

// If the -c is encountered, then we change the constant seed flag
         case 'c':
             *useConstantSeed = 1;
             break;

case ':':
             printf("Missing arg for %c\n", optopt);
             Usage(argv[0]);
             exit(EXIT_FAILURE);
             break;

case '?':
             if (
                 (optopt == 'v') ||
                 (optopt == 't')
             )
             {
             Usage(argv[0]);
             exit(EXIT_FAILURE);
             } else if (isprint (optopt)) {
             fprintf (stderr, "Unknown option `-%c'.\n", optopt);
             Usage(argv[0]);
             exit(EXIT_FAILURE);
             } else {
             fprintf (stderr,
                     "Unknown non-printable option character `\\x%x'.\n",
                     optopt);
             Usage(argv[0]);
             exit(EXIT_FAILURE);
             }
             break;

}
     }
 }

// Check a string as a number containing all digits
 int isNumber(char s[])
 {
     for (int i = 0; s[i]!= '\0'; i++)
     {
         if (isdigit(s[i]) == 0)
             return 0;
     }

return 1;
 }

// Called when isNumber() fails
 void exitWithError(char cmdFlag, char ** argv) {
     fprintf(stderr, "Option -%c needs a number value\n", cmdFlag);
     Usage(argv[0]);
     exit(EXIT_FAILURE);
 }

void Usage(char *program) {
     fprintf(stderr, "This program demonstrates use of a loop to create a stream of random numbers in a sequential fashion.");
     fprintf(stderr, "\nUsage: %s [-h] [-n numReps][-c]\n", program);
     fprintf(stderr, "   -h shows this message and exits.\n");
     fprintf(stderr, "   -n indicates the number of repetitions of the loop (default is 8).\n");
     fprintf(stderr, "   -c indicates that a fixed seed will be used, resulting in the same stream of numbers each time this is run.\n");
 }

Use of trng in parallel programs¶

The goal of the trng library is to be able to produce the same set of random numbers as the sequential version when given the same seed.

Warning

The key word above is set. The random numbers will be the same overall for the same number of repetitions, but the threads will run independently and get a different portion of a stream that matches the sequential version. In addition, the threads don’t run in any particular order, so the stream of random numbers becomes a set with the same values as the stream.

Two independent aspects of creating the parallel version¶

As with many sequential versions of programs, we can change the original version into a parallel version. In this case with random numbers, we have two separate tasks to accomplish:

Use openMP pragmas and functions to fork a set of threads and use data decomposition with a parallel for loop to ensure each thread generates a roughly equal portion of the random values. We have seen two ways of implementing a parallel for loop to split the work:

Break the original sequential loop into equal chunks (or off by at most one iteration of the loop). In the patternlets chapter, we called this “equal chunks”

Change the loop structure to have each thread do one of the first numThreads iterations, then skip ahead by numThreads. We’ve called this “chunks of one”.

Use the parallelism features of the trng library to ensure that each thread gets a substream of the original stream of random numbers. As mentioned above, this is actually a subset of the original stream, because the ordering is not necessarily preserved from the original stream, yet the values are. There are two ways that the programmer can signify this separation of the random number stream onto each thread:

“Leapfrogging”: each thread gets one number from the stream, then advances by the total number of threads to get the next number. This is illustrated as follows for 4 threads:

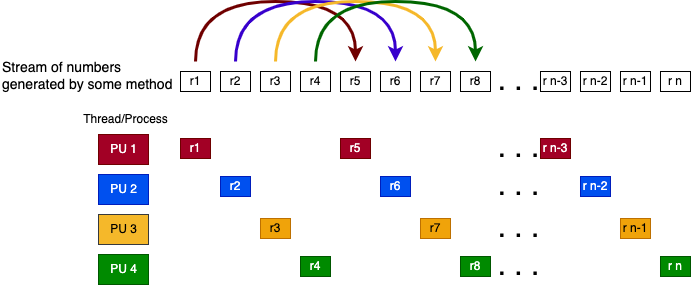
“Block splitting”: each thread is assigned an equal successive portion of stream. For 4 threads and 12 random number in the stream show this as follows:

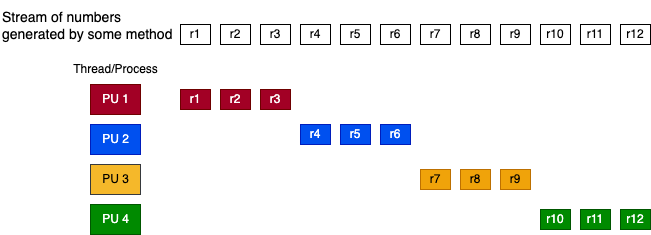
Later you will see why we chose to fix the amount of random numbers in the stream for the block splitting example. It is an important part of this method.

Warning

Because these methods for decomposing the work (A.1 and A.2 above) appear similar to the methods for doling out the random numbers, as a programmer you need to make sure that you don’t conflate them. Instead, realize that they are independent of each other.

Because these methods are independent, we can use either of the two data decomposition methods with either of the two methods for doling out the random numbers. Thus, there are a total of four possibilities for accomplishing the parallelization using openMP and the trng library. We demonstrate examples of all four possibilities here.

A.1 equal chunks with B.1 leapfrogging for random numbers
A.1 equal chunks with B.2 block splitting for random numbers
A.2 chunks of one with B.1 leapfrogging for random numbers
A.2 chunks of one with B.2 block splitting for random numbers

Note that all four examples use the same command line arguments, so we reuse the code for that (shown below them as a hidden code block).

A.1 Parallel loop with equal chunks¶

#include <stdio.h>  // printf()
 #include <time.h>   // time()
 #include <string.h> // C++ string comparison

#include <omp.h>

// trng YARN (yet another random number) generator class
 #include <trng/yarn2.hpp>
 #include <trng/uniform_dist.hpp> // we'll use a uniform distribution
                                 // of the random numbers

#define LEAPFROG 0
 #define BLOCKSPLIT 1

////////////////////////////////////////////////////////////
 int main(int argc, char *argv[])
 {

// set up what conditions we will use:
   //  - defult size of repetitions in the loop
   //  - whether to use a constant seed so we can repeat and
   //    get same random values in stream

int repetitions = 8;
   int useConstantSeed = 0; // for same stream, set this to 1 on cammand line with -c
   int verbose = 0;
   // rnage for uniform distribution of random numbers
   int min = 1;
   int max = 99;

// method the random generator will use to dole out the numbers
   int doleOut = LEAPFROG;

// for openMP
   int numThreads = 1;

// gather command line arguments
   getArguments(argc, argv, &numThreads, &repetitions,
               &useConstantSeed, &doleOut);

// openMP additions +++++++++++++++++++++++++++++++++++++++++++
   int tid = 0;
   omp_set_num_threads(numThreads);
   // Print out info
   printf("trng random number stream will be split ");
   if (doleOut == LEAPFROG)
   {
     printf("using leapfrog.\n");
   }
   else
   {
     printf("into blocks.\n");
   }
   printf("The loop is partitioned into equal chunks per thread.\n");
   printf("This means that the loop indices should be consecutive per thread.\n");
   printf("the output is printed like this:\n");
   printf("thread (loop index):randNumber\n");
   // openMP additions +++++++++++++++++++++++++++++++++++++++++++++

// ///////////////  random generator setup /////////////////////

// random numbers start from a seed value
   long unsigned int seedValue; // note for trng this is long unsigned

// For threaded openMP version, each thread will fork and have
 // a private copy of:
 //
 //  its thread id
 //
 // These are also automatically private because they are
 // declared inside the pragma block:
 //  -the generator and the distribution
 //  -the next value that will comback from the generator via the distribution
 //  -the loop counter
 //
 //  Since seedValue and repetitions are read but not written,
 //  they are shared.
 //
 // //////////////   begin fork here by using pragma for the compiler
 #pragma omp parallel default(none) private(tid) \
     shared(seedValue, repetitions, min, max, numThreads, doleOut)
   {
     // number generation needs two things: a generator and a distribution of the numbers
     // declare the generator object
     trng::yarn2 randGen;
     // declare the distribution to use (here it is uniform with vallues in the range min to max)
     trng::uniform_dist<> uniform(min, max);

// Set the starting point of the generator by seeding it
     randGen.seed(seedValue);

// OpenMP addition: get my thread number
     tid = omp_get_thread_num();

// Addition for openMP and parallel in general: the generator must be set to give
     // the thread its portion of the random numbers.
     // Note if single thread, this isn't necessary.
     if (numThreads > 1)
     {
       if (doleOut == LEAPFROG)
       {
         // thread will get substream tid from numThread separate substreams
         randGen.split((unsigned)numThreads, tid); // this is the leapfrog setup
       }
       else
       {
         // thread will get substream as a block:
         // thread 0 starts at 0, thread 1 starts at repetitions / numThreads, etc.
         randGen.jump(tid * (repetitions / numThreads)); // block split
       }
     }
     // //////////////// end PRNG setup /////////////////////////////////

// //////////////// get a portion of the stream /////////////////////
     int nextRandValue; // holds the next value as we go through the loop

// loop to get each number in the PRNG stream and print it
     // Note here the ubiquitous for loop construction of incrementing by 1-
     //   this leads itself nicely to letting the openMP compiler split the
     //   loop into equal chunks using the pragma shown.
     int i;
 #pragma omp for
     for (i = 0; i < repetitions; i++)
     {
       // get next number in the stream from the distribution
       nextRandValue = uniform(randGen);
       // print tid(i):nextRandValue
       printf("t%2d (%2d):%2d \n", tid, i, nextRandValue);
     }

} // end of parallel block

return 0;
 }

As a reference, here is the set of numbers when using one thread with a given constant seed:

t 0( 0):83
t 0( 1):63
t 0( 2):97
t 0( 3):21
t 0( 4):62
t 0( 5):54
t 0( 6):14
t 0( 7):46

This is an OpenMP version with the following command line arguments:

-t indicates number of threads to use.
-n indicates the number of repetitions of the loop (default is 8).
-c indicates that a fixed seed will be used, resulting in the same
   stream of numbers each time this is run.
-d indicates whether the trng generator will dole out numbers in
   block or in leapfrog fashion. default is leapfrog.

Study the code by reading the comments. Note in particular:

The pragma for the parallel block where the threads fork is separated from a pragma for the parallel for loop.
All threads are executing setup code for the generation of random numbers.
You must NOT indicate block splitting or leapfrog if you are only using one thread. This is assured by code beginning on line 109.

Note

This is an important new aspect of how we can and need to change this type of code by separating some lines of code that are done on each thread when they fork before the loop is decomposed onto each thread (requiring a second pragma).

This syntax is tricky for newcomers to OpenMP. The inner pramga is simply ‘#pragma omp for’ without the keyword parallel, which has already been placed in the previous pragma to indicate where the threads fork.

Try running the code above with these arguments (which are the original ones on this page if you reload it):

['-c', '-n 8', '-d block', '-t 1']

You should see that we are able to replicate the same set of numbers as the sequential version using this OpenMP version with one thread.

Now try changing the command line arguments in the above code block to use two threads, like this:

['-c', '-n 8', '-d block', '-t 2']

You should still get the same set of numbers. Now try using 4 threads, like this:

['-c', '-n 8', '-d block', '-t 4']

These examples have been using block splitting for the method of doling out portions of the stream of numbers to the threads. One important rule about using this particular method is that the set of numbers must be equally divisible by the number of threads that you use. To see how this method can fail, try this:

['-c', '-n 8', '-d block', '-t 3']

What do you observe?

Warning

You must be very careful when using block splitting, because the code will run, but the results are incorrect when the number of numbers in the stream is not divisible by the number of threads.

Next try leapfrog by trying these command line arguments:

['-c', '-n 8', '-d leapfrog', '-t 1']
['-c', '-n 8', '-d leapfrog', '-t 2']

Notice a couple of things about using 2 threads with leapfrogging:

Thread 0 should get every other number starting from loop index 0: 83, 97, 62, 14
Thread 1 should get every other number starting from loop index 1: 63, 21, 54, 46
Since the OpenMP pragma and the for loop uses data decomposition of equal chunks of the loop per thread, then thread 0 gets loop indices 0, 1, 2, and 3, and thread 1 gets loop indices 4, 5, 6, and 7.
The order in which the threads complete is not guaranteed. Luckily, many applications do not rely on this (it’s random numbers, after all).

Now try different numbers of threads, like this:

['-c', '-n 8', '-d leapfrog', '-t 4']
['-c', '-n 8', '-d leapfrog', '-t 3']

Study the results of each to see that the leapfrogging is working as you would expect.

Notice that although the total number of numbers in the stream is not divisible by 3 threads, the set of numbers generated is the same.

Note

These last few examples show that leapfrogging can be a safer alternative when you may vary how many numbers you generate and how many threads you use.

A.2 Parallel loop with chunks of one¶

#include <stdio.h>        // printf()
 #include <time.h>        // time()

#include <omp.h>

#define LEAPFROG 0
 #define BLOCKSPLIT 1

////////////////////////////////////////////////////////////
 int main(int argc, char* argv[]) {

// set up what conditions we will use:
   //  - defult size of repetitions in the loop
   //  - whether to use a constant seed so we can repeat and
   //    get same random values in stream

int repetitions = 8;
   int useConstantSeed = 0; // for same stream, set this to 1 on cammand line with -c

// rnage for uniform distribution of random numbers
   int min = 1;
   int max = 99;
   // for method the random generator with use to dole out the numbers
   int doleOut = LEAPFROG;

// for openMP
   int numThreads = 1;

// gather command line arguments
   getArguments(argc, argv, &numThreads, &repetitions, &useConstantSeed, &doleOut);

// openMP additions +++++++++++++++++++++++++++++++++++++++++++
   int tid =0;
   omp_set_num_threads(numThreads);
   // Print out info
   printf("trng random number stream will be split ");
   if (doleOut == LEAPFROG) {
     printf("using leapfrog.\n");
   } else {
     printf("into blocks.\n");
   }
   printf("The loop is partitioned into chunks of 1 per thread.\n");
   printf("This means the loop index for each thread starts at its tid and updates by the number of threads.\n");
   printf("the output is printed like this:\n");
   printf("thread (loop index):randNumber\n");
   // openMP additions +++++++++++++++++++++++++++++++++++++++++++++

// /////////////////  random generator setup /////////////////////

// random numbers start from a seed value
   long unsigned int seedValue;  // note for trng this is long unsigned

// For threaded openMP version, each thread will fork and have a private copy of:
 //
 //  its thread id
 //
 // These are also automatically private because they are declared inside the pragma block:
 //  -the generator and the distribution
 //  -the next value that will comback from the generator via the distribution
 //  -the loop counter
 //
 //  Since seedValue and repetitions are read but not written, they are shared.
 //
 // ////////////////////   begin fork here by using pragma for the compiler
 #pragma omp parallel default (none) \
 private(tid) \
 shared(seedValue,repetitions, min, max, numThreads, doleOut)
   {
     // number generation needs two things: a generator and a distribution of the numbers
     // declare the generator object
     trng::yarn2 randGen;
     // declare the distribution to use (here it is uniform with vallues in the range min to max)
     trng::uniform_dist<> uniform(min, max);

// Set the starting point of the generator by seeding it
     randGen.seed(seedValue);

// OpenMP addition: get my thread number
     tid = omp_get_thread_num();

// Addition for openMP and parallel in general: the generator must be set to give
     // the thread its portion of the random numbers.
     // Note if single thread, this isn't necessary.
     if (numThreads > 1) {
       if (doleOut == LEAPFROG) {
         // thread will get substream tid from numThread separate substreams
         randGen.split((unsigned)numThreads, tid);  // this is the leapfrog setup
       } else {
         // thread will get substream as a block:
         // thread 0 starts at 0, thread 1 starts at repetitions / numThreads, etc.
         randGen.jump(tid * (repetitions / numThreads));   // block split
       }
     }
     // /////////////////////// end PRNG setup ///////////////////////////////////

// /////////////// get a portion of the stream //////////////////////////////
     int nextRandValue;   // holds the next value as we go through the loop

// loop to get each number in the PRNG stream and print it
     // Note here a different loop structure- programmer decides which
     // parts of the loop a thread will complete.
     int i;
   // no openMP pragma for this version
     for (i=tid; i < repetitions; i+=numThreads) {
       // get next number in the stream from the distribution
       nextRandValue = uniform(randGen);
       // print tid(i):nextRandValue
       printf("t%2d(%2d):%2d \n", tid, i, nextRandValue);
     }

} // end of parallel block

return 0;
 }

As a reference, here is the set of numbers when using one thread, which is the same as the sequential version:

t 0( 0):83
t 0( 1):63
t 0( 2):97
t 0( 3):21
t 0( 4):62
t 0( 5):54
t 0( 6):14
t 0( 7):46

You should study the code for this version, focusing on the for loop and how it differs from the previous version.

Note

Rule of thumb: splitting a for loop into equal chunks requires the #pragma omp for syntax. You do not use this syntax if you move forward the proper amount per thread yourself in the code.

Now try different setups for this code, as you did for the equal chunks version:

['-c', '-n 8', '-d block', '-t 2']
['-c', '-n 8', '-d block', '-t 4']
['-c', '-n 8', '-d leapfrog', '-t 2']
['-c', '-n 8', '-d leapfrog', '-t 4']
['-c', '-n 8', '-d leapfrog', '-t 3']

Note that the output is explaining how it is running. You should be able to observe the following:

With block splitting and 2 threads, thread 0 still gets the first block of 4 values from the sequential version, and thread 1 gets the next block, even though the loop indexes it completes are different from the previous equal chunk loop version.
With leapfrog and 2 threads, each thread gets the same numbers as the equal chunk loop version:
- Thread 0 should get every other number: 83, 97, 62, 14
- Thread 1 should get every other number: 63, 21, 54, 46
Leapfrog works with 3 threads

Conclusion: four different ways to accomplish the same task, but use with caution!¶

The bottom line with these examples is that when we have added the complexity of 2 possible ways for trng to decide which thread gets which number from the stream with two possible ways of decomposing the repetitions of a loop, we end up with four ways to achieve the same ultimate task.

Which method to use depends on the situation you are faced with. As a general rule, we often use equal chunks for decomposition because it matches the sequential version and the work being done inside the loop is roughly the same for each iteration. However, if the amount of work varies in each loop iteration, then “chunks of one” can be more effective. We have to combine it with a mechanism for letting more threads do more iterations if they are ready for work. This is called dynamic thread assignment.

When it comes to doling out the random numbers to the threads, the choice is somewhat important. Block splitting makes sense when the iterations can be equally divided by the treads (what happened when you chose 3 threads?). Leapfrog works even if each thread does not do exactly the same number of iterations of the loop. This is often the case, so most of the time the leapfrog method becomes the proper choice.

Command line code for reference¶

This code block below has code for handling the command line arguments for the parallel versions above. You can study it if you want to see how it was done.

void getArguments(int argc, char *argv[],
                 int * numThreads, int * N, int * useConstantSeed, int * doleOut);

int isNumber(char s[]);
 void exitWithError(char cmdFlag, char ** argv);
 void invalidChoice(char cmdFlag, char ** argv);
 void Usage(char *program);

#include <stdio.h>
 #include <unistd.h>
 #include <stdlib.h>
 #include <ctype.h>
 #include <string.h>  // C++ string comparison

#define LEAPFROG 0
 #define BLOCKSPLIT 1

void getArguments(int argc, char *argv[],
                   int * numThreads, int * N, int * useConstantSeed, int * doleOut)
 {

int c;        // result from getopt calls

// The : after a character means a value is expected
   // No colon means it is simply a flag with no associated value
   while ((c = getopt (argc, argv, "n:t:d:hc")) != -1) {

// getopt implicitly sets a value to a char * (string) called optarg
 // to what the user typed after -n
     switch (c)
       {
       // character string entered after the -N needs to be a number
       case 'n':
         if (isNumber(optarg)) {
           *N = atoi(optarg);
         } else {
           exitWithError(c, argv);
         }
         break;

// character string entered after the -t needs to be a number
       case 't':
         if (isNumber(optarg)) {
           *numThreads = atoi(optarg);
         } else {
           exitWithError(c, argv);
         }
         break;

case 'd':
         if (strcmp(optarg, "block") == 0) {
           *doleOut = BLOCKSPLIT;
         } else if (strcmp(optarg, "leapfrog") == 0) {
           *doleOut = LEAPFROG;
         } else {
           invalidChoice(c, argv);
         }
         break;
       // If the -h is encountered, then we provide usage
       case 'h':
         Usage(argv[0]);
         exit(0);
         break;

// If the -c is encountered, then we change the constant seed flag
       case 'c':
         *useConstantSeed = 1;
         break;

case ':':
         printf("Missing arg for %c\n", optopt);
         Usage(argv[0]);
         exit(EXIT_FAILURE);
         break;

case '?':
         if (
             (optopt == 'v') ||
             (optopt == 't')
           )
         {
           Usage(argv[0]);
           exit(EXIT_FAILURE);
         } else if (isprint (optopt)) {
           fprintf (stderr, "Unknown option `-%c'.\n", optopt);
           Usage(argv[0]);
           exit(EXIT_FAILURE);
         } else {
           fprintf (stderr,
                   "Unknown non-printable option character `\\x%x'.\n",
                   optopt);
           Usage(argv[0]);
           exit(EXIT_FAILURE);
         }
         break;

}
   }
 }

// Check a string as a number containing all digits
 int isNumber(char s[])
 {
     for (int i = 0; s[i]!= '\0'; i++)
     {
         if (isdigit(s[i]) == 0)
               return 0;
     }

return 1;
 }

// Called when isNumber() fails
 void exitWithError(char cmdFlag, char ** argv) {
   fprintf(stderr, "Option -%c needs a number value\n", cmdFlag);
   Usage(argv[0]);
   exit(EXIT_FAILURE);
 }

void invalidChoice(char cmdFlag, char ** argv) {
   fprintf(stderr, "unrecognized value for Option -%c needs 'block' or 'leapfrog'\n", cmdFlag);
   Usage(argv[0]);
   exit(EXIT_FAILURE);
 }

void Usage(char *program) {
   fprintf(stderr, "This program demonstrates use of a loop to create a stream of random numbers in parallel.\n");
   fprintf(stderr, "Usage: %s [-h] [-t numThreads] [-n numReps][-c] [-d block|leapfrog]\n", program);
   fprintf(stderr, "   -h shows this message and exits.\n");
   fprintf(stderr, "   -t indicates number of threads to use.\n");
   fprintf(stderr, "   -n indicates the number of repetitions of the loop (default is 8).\n");
   fprintf(stderr, "   -c indicates that a fixed seed will be used, resulting in the same stream of numbers each time this is run.\n");
   fprintf(stderr, "   -d indicates whether the trng generator will dole out numbers in blocks or in leapfrog fashion. default is leapfrog.\n");
 }

You have attempted of activities on this page