3.2 Parallel Random Number Generation with trng¶
Now that you have seen the sequential method for using the new trng library in a loop, we will show four distinct methods that can be used to properly generate the same stream of numbers in parallel for that same example.
In this section we introduce simple code examples to illustrate what types of patterns are often seen in real PDC examples. You should note that the primary use of PRNGs in parallel applications is to generate one after another in a loop. Recall that you have already seen how to decompose loops in shared memory with OpenMP in the previous chapter: equal chunks and chunks of one.
Use of trng in parallel programs¶
The goal of the trng library is to be able to produce the same set of random numbers as the sequential version when given the same seed.
Warning
The key word above is set. The random numbers will be the same overall for the same number of repetitions, but the threads will run independently and get a different portion of a stream that matches the sequential version. In addition, the threads don’t run in any particular order, so the stream of random numbers becomes a set with the same values as the stream.
Two independent aspects of creating the parallel version¶
As with many sequential versions of programs, we can change the original version into a parallel version. In this case with random numbers, we have two separate tasks to accomplish:
Use openMP pragmas and functions to fork a set of threads and use data decomposition with a parallel for loop to ensure each thread generates a roughly equal portion of the random values. We have seen two ways of implementing a parallel for loop to split the work:
Break the original sequential loop into equal chunks (or off by at most one iteration of the loop). In the patternlets chapter, we called this “equal chunks”
Change the loop structure to have each thread do one of the first numThreads iterations, then skip ahead by numThreads. We’ve called this “chunks of one”.
Use the parallelism features of the trng library to ensure that each thread gets a substream of the original stream of random numbers. As mentioned above, this is actually a subset of the original stream, because the ordering is not necessarily preserved from the original stream, yet the values are. There are two ways that the programmer can signify this separation of the random number stream onto each thread:
“Leapfrogging”: each thread gets one number from the stream, then advances by the total number of threads to get the next number. This is illustrated as follows for 4 threads:
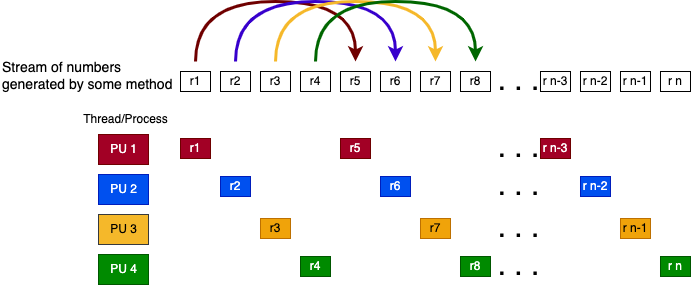
“Block splitting”: each thread is assigned an equal successive portion of stream. For 4 threads and 12 random numbers in the stream the distribution is as follows:
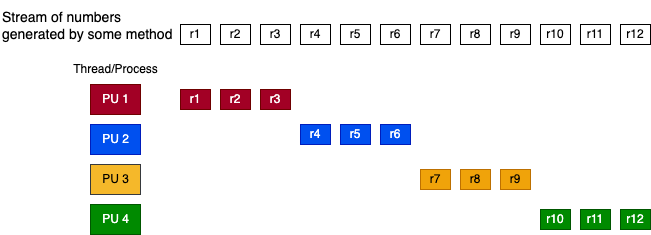
Warning
Because these methods for decomposing the work (A.1 and A.2 above) appear similar to the methods for doling out the random numbers, as a programmer you need to make sure that you don’t conflate them. Instead, realize that they are independent of each other.
Because these methods are independent, we can use either of the two data decomposition methods with either of the two methods for doling out the random numbers. Thus, there are a total of four possibilities for accomplishing the parallelization using openMP and the trng library. We demonstrate examples of all four possibilities here.
A.1 equal chunks with B.1 leapfrogging for random numbers
A.1 equal chunks with B.2 block splitting for random numbers
A.2 chunks of one with B.1 leapfrogging for random numbers
A.2 chunks of one with B.2 block splitting for random numbers
Note that all four examples use the same command line arguments, so we reuse the code for that (shown later them as a hidden code block).
