8.2. Forest Fire Simulation Example

Note

You should use the VNC connection to the head node of your Raspberry Pi cluster, because this example produces graphical output.

This example was ported to Python by Libby Shoop (Macalester College), from the original Shodor foundation C code example.

According to the above Shodor page:

“You can run a single instance of a forest fire simulation in which a forest is modeled as an \(N \times N\) grid of trees. One tree starts to smolder, and each iteration nearby trees have some chance of catching fire. The model follows the following rules:”

• Burning trees burn down.

• Smoldering trees catch fire.

• Unburnt trees next to (N, S, E, W) a burning tree catch fire with some random probability less than or equal to a given probability threshold.

• Repeat until fire burns out.

The main input parameters for the model are:

• The size, \(N\) of one row of trees in the \(N \times N\) grid representing part of the forest.

• The upper limit of the chance of the fire spreading from a burning tree to a nearby unburnt tree.

The simulation starts with the tree in the center of the grid smoldering, and all other trees alive.

The main outputs for the single fire model are:

• The percentage of additional trees burned beyond the first tree.

• The number of iterations before the fire burns out.

One single instance of this model can produce a different result each time it is run because of the randomness of the probability of unburnt trees catching fire.

8.2.1. Overview of Code

You can access the C forest fire simulation from the head node of the CSinParallel Raspberry Pi cluster by navigating to the mpiFire_C directory under Exemplars/MPI_examples:

cd CSinParallel/Exemplars/MPI_examples/mpiFire_C

The folder called mpiFire_C has a simple simulation of the spread of a wildfire in a forest.

• oneFire.c runs a single model of a fire starting from one tree and burning until it is out.

• seqFireSim.c runs many of the above single model cases for many ‘trials’ and averages the results to get a reasonable overall behavior of a fire at different thresholds of probability that fire will spread from one tree to another.

• mpiFireSim.c does the same simulation as the above sequential version, but uses parallelism to split the number of trials among processes.

8.2.2. Patterns used

The mpi version of the simulation uses these patterns from the mpi4py patternlets:

• SPMD, Single program, multiple data

• Decompose the work using parallel loop of equal chunks

• Message passing

Study the file mpiFireSim.c in an editor to find these. Or you could do that later and simply see how the code performs by running it as described below.

8.2.3. Compile with make

Simply type make at the command line to build all the versions of this code.

8.2.4. Running the Code (Sequential Version)

The code in oneFire.c creates a visualization serially that looks somewhat like the following, with \(N\) = 25 and the probability threshold = 0.4.

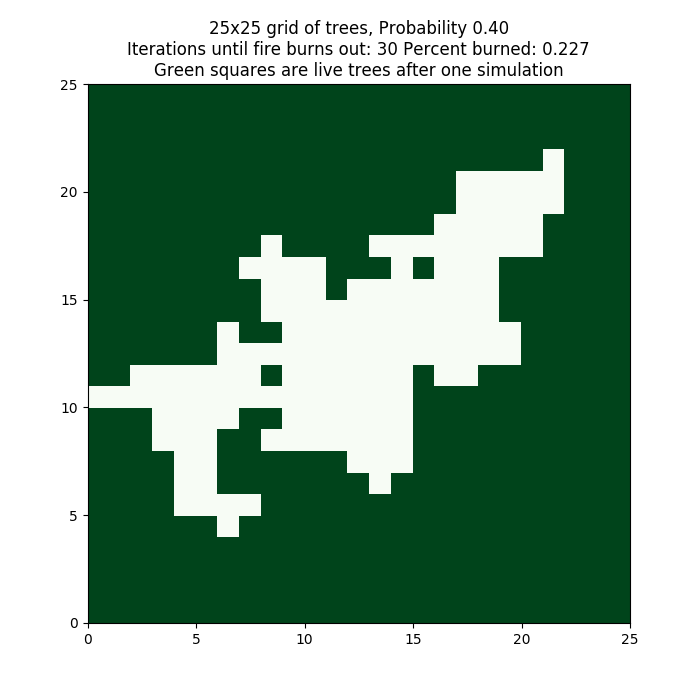
Output like this can be obtained by running the single model like this:

./oneFire 25 0.4

Note

The resulting plot can be closed by clicking the X icon in the upper left of the window that pops up. The terminal prompt will also ask you to hit enter to continue. You can hit enter at the terminal with the plot still up, and it will close it.

Try running this several times at the same 0.4 threshold. Then try varying the threshold from 0.2 to 1.0 by 0.1 increments.

Each time the code is run, the result could be different. In addition, even if we ran several trials, the resulting percent of trees burned and number of iterations before the fire burned out on average would be different, depending on the input probability threshold. Because of this, a more realistic simulation requires that many instances of the above single simulation be run in this way:

• Keep the size of the grid of trees the same.

• Start with a low probability threshold.

• Run a given number of trials at a fixed probability threshold.

• Repeat for another probability threshold, some increment larger than the previous one, until the threshold is 1.0.

This simulation of multiple trials at a range of different probability thresholds has a known interesting output, which can be graphed as follows:

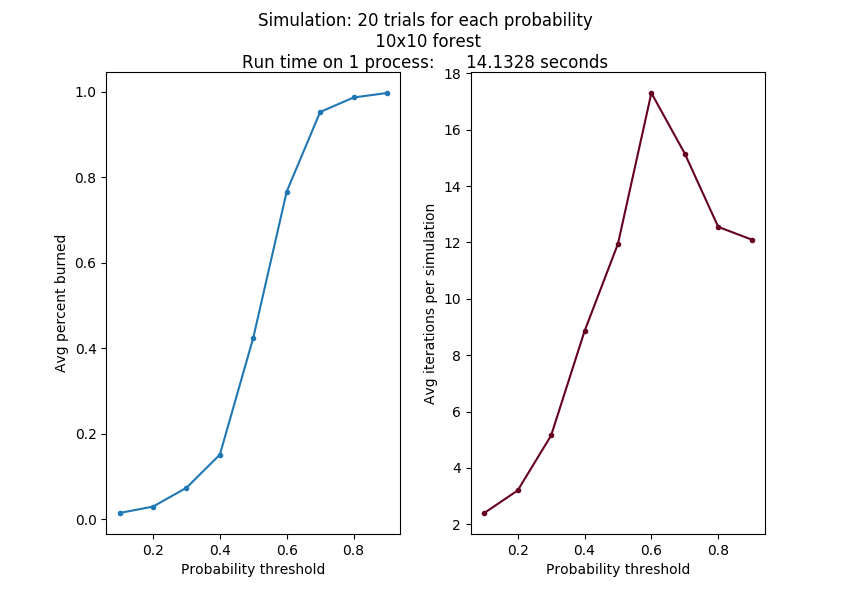
In this case, we ran 20 trials on a single Raspberry Pi 3B, with the probability threshold starting at 0.1 and incrementing by 0.1. You can do something similar to this running by the code file seqFireSim on a cluster head node like this:

./seqFireSim 20 30 11 1

Unlike the image above, this C code creates separate windows for each plot. This example above was for 30 trials on a \(20 \times 20\) forest using a total of 11 probability thresholds between 0 and 1. The last argument signifies that we want to display the plots.

As the size of the grid changes and the probability points increase, these curves will look roughly the same, although they should get smoother as the number of trials increases and the increment value is smaller. But these more accurate simulations take a long time to run.

8.2.5. The parallel MPI version

The desired outcome of the parallel version is to also produce a plot of average percent burns as a function of probability of spreading, as quickly and as accurately as possible. This should take into account that the probability of the fire spreading will affect not only how long it takes for the fire to burn out but also the number of iterations required to reached an accurate representation of the average.

If we put more processes to work on the problem, we should be able to complete a more accurate simulation in less time than the sequential version. Even the same problem as above produced the same results running on 4 processes on different nodes of a cluster in almost 1/4 of the time. Its output looks like this:

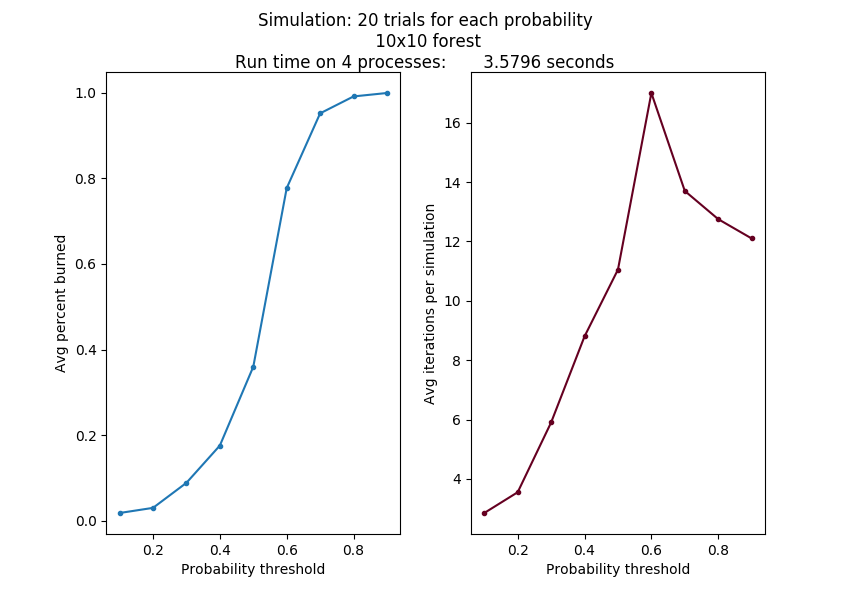
This can be run like this, with more trials and more probability values:

mpirun -np 4 ./mpiFireSim 20 100 101 1

The parallelization happens by splitting up the number of trials to be run among the processes. Each process completes the range of probabilities for its portion of the trials, sending the results back to the conductor process.

8.2.5.1. Try some other cases to observe how it scales

Ideally, as you double the number of workers on the same problem, the time should be cut in half. This is called strong scalability. But there is some overhead from the message passing, so we don’t often see perfect strong scalability.

Try running these tests, where the number of workers is one less than the number of processors from the -np value:

-np	tree row size	number of trials	probability thresholds	running time
3	20	1200	101
5	20	1200	101
9	20	1200	101

What do you observe about the time as you double the number of workers?

When does the message passing cause the most overhead, which adds to the running time?

Try some other cases of your own design.

You have attempted of activities on this page